[Exploration Method] Smooth Exploration for Robotic ReinforcementLearning

논문: https://arxiv.org/pdf/2005.05719
 

논문에 대한 간략 설명

강화학습 하면 생각나는게 두 가지가 있다.
첫 번째로 대표적인 강화학습 pytorch library인 Stable-baselines3
두 번째로 Exploration과 Exploritation
 
해당 논문은 Stable-baselines3를 만든 사람이 낸 논문이다.
Exploration 중에 robotics에 관련한 방법론을 제시한 논문이다.
 
강화학습을 사용해보았던 모든 이들에게 아래와 같은 문제가 되는 것이 있을 것이다.
 

강화학습을 적용하기에는 비현실적인 행동[Shaky behavior]이 너무 많다.

 
해당 논문은 위와 같은 원인을 Exploration에 있다고 본다.
 
따라서 본 논문은 이를 해결하기 위한 새로운 Exploration 기법은 State-Dependent Exploration을 제시한다.
해당 논문의 특징은 DDPG와 같은 Off-policy 뿐만 아니라 PPO와 같은 On-policy에도 사용할 수 있다는 장점이 있다.
또한 Stable-baselines3에서 간단하게 아래와 같은 parameters를 설정하면 사용할 수 있다는 장점이 있다.
1. use_sde
2. log_std_init
3. sde_sample_freq

기존의 Exploration

기존의 Exploration은 ,특히 action space가 continous, Gaussian noise를 첨가하여 행동을 장려한다.
대표적으로 DDPG가 있다. 해당 방법을 본 논문에선 Step based Unstructured Exploration이라고 한다.
탐험을 많이 할 수 록 RL의 성능이 상승한다는 것은 누구나 알고 있는 사실이지만.. 해당 방법 시간[time]에 독립적이다.
즉, Gaussian noise가 계속해서 첨가된다는 점이 있다. [그림 1]을 참고
이러한 noise가 앞서 언급한 Shaky behavior를 만들어낸다고 본 논문은 설명한다.

[그림 1]

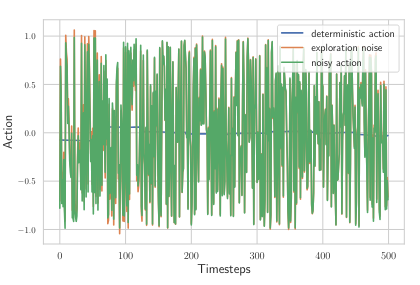
Shaky Behavior의 문제점

이러한 비현실적인 움직임이 왜 문제가 되냐고 생각할 수 있을 것이다.
간단한 예시로 자율주행 로봇이 제어할 수 있는 가속도 범위가 정해져 있는데 이를 무시하고 컨트롤하는 경우가 존재한다.
이렇게 되면 주행 성능은 좋을지 언정, 오히려 모터에 무리가 많이가버려 유지보수에 많은 비용이 들 것이다.
즉, 빛좋은 개살구다.
 

State-Dependent Exploration

Exploration in Action or Policy Parameter Space

기존의 Exploration과 동일하게 각 step t마다 독립적으로 Gaussian distribution으로 부터 noise를 추출한다.
이후 deterministic policy에 덧셈을 하여 [Gaussian distribution은 합 연산에 열려있다.] Stochastic policy를 얻는다.
수식은 아래와 같다.
 
Deterministic Policy: $a^{deter}_t = μ(s_t; θ_μ)$, Noise: $\epsilon_t $ ~ $N[0,\sigma^2]$
위 수식을 더하면 다음과 같은 Stochastic Policy를 얻을 수 있다.
Stochastic Policy: $a_t = μ(s_t; θ_μ) + \epsilon_t$
 
간단한 방법 같지만 해당 방법은 많은 양의 parameter가 요구된다고 한다.
 

State-Dependent Exploration [SDE]

본 논문의 기본 방법이다.
이름에서 부터 알 수 있듯이 본 방법은 Noise항에 State를 첨가한다.
수식은 아래와 같다.
 
Deterministic Policy: $a^{deter}_t = μ(s_t; θ_μ)$, Noise: $\theta_{\epsilon}$ ~ $N[0,\sigma^2]$
위 수식을 더하면 다음과 같은 State-Dependent Exploration Policy를 얻을 수 있다.
State-Dependent Exploration Policy: $a_t = μ(s_t; θ_μ) + \epsilon(s_t;\theta_{\epsilon})$
 
이를 매 episode 마다 샘플링하여,  mean value 근처에서 진동하는 exploration 대신, action $a$는 주어진 state $s$에 대해 동일한 값을 출력할 수 있게 할 수 있다. 즉, 더 부드럽게 exploration을 장려할 수 있다.
 
해당 방법은 일반적인 policy gradient methods에 적용이 가능하다 [즉, PPO, SAC 등 그냥 사용하면 된다.]
 

Generalized State-Dependent Exploration [gSDE]

본 논문이 제시하는 방법이다.
SDE는 그냥 쓰면 문제가 있다. 본 논문은 크게 4가지를 언급하며, 이를 해결하는 gSDE를 제시한다.
1. noise는 하나의 episode 동안 변화하지 않는다. 이는 곳 episode 길이가 길어지면, exploration이 제한된다는 문제가 된다.
2. SDE는 $\sigma$를 diagonal matrix [아래 수식 참고]로 가정하게 되는데, 초기값 설정이 각 task마다 중요해진다.
$$\sigma = [{\sum_i (\sigma s)^2}]^{0.5}$$
3. state와 exploration noise에는 단 하나의 선형적 의존성 [$ \epsilon(s_t;\theta_{\epsilon})$]만 존재하게 되므로 다양성이 죽는다.
4. gradient와 noise 크기는 state 크기에 따라 달라지므로 state는 normalize 해야한다.
 
해당 논문은 간단하게 위 문제들을 해결한다.
1. $\theta_{\epsilon}$ 를 매  $n$ step 마다 샘플한다. [기존 SDE는  episode 마다 샘플함] -> SDE의 1번 해결
2. $\sigma = [{\sum_i (\sigma s)^2}]^{0.5}$  수식에서 state의 $s$ 대신에 policy feature $z_{\mu} (s;\theta_z)$를 사용한다. 이는 즉, policy network의 마지막 층의 deterministic ouput인  $\mu(s) = \theta_{\mu}z_{mu}(s;\theta_z) $를 nonlinear noise function으로 사용한다는 의미이다. -> SDE의 2,3번 해결
 
주의할 점은 $n$ step에서 $n$ 의 값이 1이면.. 기존 Step based Unstructed exploration과 동일하며, $n$ 이 episode 길이와 동일하면 SDE와 같다는 것이다.
 
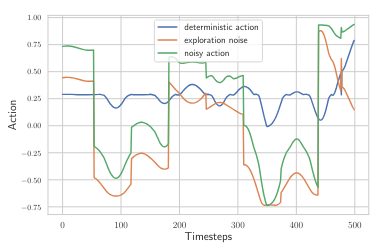
gSDE의 결과를 보자 [그림 2]참고

[그림 2]