2024. 7. 1. 19:28ㆍRLHF
논문 링크
https://arxiv.org/pdf/2305.18290
해당 리뷰는 수식 유도는 생략
Keywords:
Reinforcement Learning Human Feedback[RLHF], Point-wise comparison or Bandit, Direct Preference Optimization, Offline learning
1. Abstract
1.1. 기존 RLHF의 문제
기존 RLHF의 방법은 복잡하고 불안전한 능력을 보여줌. 해당 이유는 아래와 같음
1. 인간의 선호[preference]를 반영한 Reward model의 문제
2. 강화학습을 통해 원래의 모델을 미세 조정[fine-tuning]하는 단계에서의 문제.
1.2. 본 논문이 제시하는 바
해당 문제들을 해결하기 위해서 본 논문은 간단한 classification loss을 적용하여 해결하고자 함.
이 방법을 Direct Preference Optimization[DPO]라 명명하며, 기존 방법보다 간단하고, 안전하며, 가벼운 방법임.
2. Introduction
Abstract에 설명되어 있어 생략하고, DPO 부분만 언급
2.1. DPO의 loss는 어떻게 구성 되었는가?
기존 RLHF와 동일하게 preference model은 Bradley-Terry model을 따름. 단, 기존에는 해당 model를 reward model의 학습 loss로 구성한것에 반해, 본 논문은 model 수정하여 직접적으로 policy를 학습할 수 있게 변경함.
조금 더 설명하자면, 간단한 binary cross entropy를 preference data에 적용, 암묵적인 reward function을 통해 최적의 policy를 찾도록 함.
Related Work
4. Preliminaries
해당 부분은 RLHF의 단계를 설명
4.1. Supervised Fine-Tuning [SFT]
RLHF의 첫번째 단계로, 좋은 질의 데이터를 통해 reference model를 만드는 단계.
4.2. Preference sampling and Reward learning
1단계에서 얻은 reference model를 활용하여, prompts x에 대한 답변 두개[A, B]를 취득하여 인간이 선호하는 답변 선택.
여기서 중요한 점은 "선호는 잠재된 reward model에서 생성된 것" 이라는 가정이 있음.
본 가정을 통해 선호 데이터들을 통해 역으로 reward model를 찾을 수 있음을 의미하며, RLHF의 2번째 단계는 해당 reward model를 찾기 위한 과정임.
따라서, 이를 위해 "A>B, A가 선호되는 데이터"를 의미하며, 데이터가 선호될 분포를 계산하는 것은 Bradley-Terry [BT] 또는 Plackett-Luce ranking model 을 사용.
해당 방법은 2가지중 하나를 선택하는 것이므로 BT 이며, 2가지 이상인 경우 후자 model을 사용

그런 다음 reward model의 분포 추정하기 위해 maximum likelihood를 사용. [즉, 모수 분포의 모수 파라미터를 찾겠다.]
해당 문제를 다시 정리하면, Binary Classification 문제로 정의할 수 있으며, 이를 이용하면, Negative log-likelihood loss로 해결할 수 있음.

참고로 reward model의 initialize는 종종 reference model weight를 가져와 최 끝단에 linear layer 를 추가하는 경우도 있음.
이외에는 그냥 처음부터 학습 [initialize epoch 200 정도로..]
위와 같이 점추정[point estimation]을 통한 reward model은 해당 추정의 특성상 모든 데이터를 볼 수 없기 때문에 불안정성이 크며, 동시에 다음 단계인 3단계의 학습을 불안전하게 만들 수 있음.
그러므로 아래의 수식을 통해 reward model를 nomalizing 함과 동시에 낮은 분산을 [반대로 높은 편향을] 가지게 함.
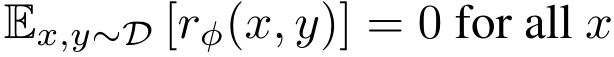
4.3. RL optimization
아래 수식을 통해 RLHF의 최종단계인, Fine-Tuning 단계를 거치는 것을 볼 수 있음.

여기서 빨간색은 이전 review의 주요 문제점인 Distribution Shift로 인한 Out-Of-Distribution, 그러니까 reward model이 보지못한 데이터에 대해 잘못된 결과를 출력하는 것을 어느정도 방지해주는 부분이라고 해석 가능하며, 동시에 RL의 state-action distribution에 대해서도 방지해줄 수 있음.
5. Direct Preference Optimization [DPO]
RL training loop 없이, 즉 3단계인 RL optimization 없이 학습하는 방법을 소개함.
이를 가능케 하기 위해, reward function을 optimal policy로 분석적으로 mapping 하는 방법을 보여줌.
즉, Policy network 만으로도 충분히 [암묵적인] reward를 나타낼 수 있음을 보여줌.
5.1. Deriving the DPO objective
증명 생략 [see Appendix A.1]
5.1.1. Partition Function

수식은 위와 같음. 참고로 Partition Function은 Soft Actor Critic 에서도 나온다!.
해당 수식을 안다는 것은 그 계를 안다는 것과 동등한데, 이는 확률 또는 정보이론에서는 간단히 시행횟수 그러니까 확률 분포의 크기로 볼 수 있음.
즉, 확률을 나타내는데 사용되는 정규화 인자 [Normalization factor] [그러니까 분모 term!]
확률로 나타내는 것은 아래 수식을 통해 알 수 있음.

5.1.2. Bradley-Terry model to Policy loss object
증명 생략 [see Appendix A.2]

위 수식은 기본 형태가 Sigmoid 형태이므로 다음과 같이 나타내어 loss object으로 표현할 수 있음.

참고로 BT model 뿐만 아니라 Appendix A.3 을 보면 Plackett-Luce ranking model 에 대한 증명도 있음.
5.2. What does the DPO update do?
그렇다면 DPO loss function은 어떤 것을 업데이트를 할까?

그러니까 선호되는 행동에 대한 Likelihood를 최대화 하고, 선호되지 않는 행동에 대한 Likelihood 최소화하여
즉, 선호되는 행동에 대한 모수 파라미터를 점추정하고 이에 대한 행동을 극대화[모델이 쫓도록] 하겠다.

'RLHF' 카테고리의 다른 글
| [RLHF] β-DPO: Direct Preference Optimizationwith Dynamic β (0) | 2024.09.04 |
|---|---|
| [RLHF] Direct Preference-based Policy Optimization without Reward Modeling (0) | 2024.07.04 |